Practically, miners do not need much knowledge of calculus, they just include transactions into the block by the ordering of fee per byte. As transactions of zero sat per byte is no beneficial and only increase the possibility of doing mining job without payoff, miners will not accept zero-fee transactions. As the block is getting bigger with higher lucrative transactions till the size with the highest expected value of the block fee, the miners stop including additional lower fee transactions into the block. The theoretical analysis is as below.

By knowledge mentioned in EstimateBlockFee and BlockIntervalTime, one can derive the optimal ratio about the delayed time of block propagation. When miners assess zero revenue for orphan probability and aims to maximize the the expected value of the block fee, they come to maximize

or in case of exponential payment distribution:

With x being defined such x = B / MT = ND / M and k being defined k = M / DnA , this formula is translated to

which is maximized at x when

When k is large, the optimal x approaches zero. As mentioned in a long run the n or A may adapt with the x decided by the miners to have long term kx being 1 and then the expected value becomes

More precisely, the orphan does not necessarily mean zero revenue because either chain might lose or not. With knowledge mentioned in ScaleDebate, the overall impact is the reduced coin price and production efficiency and the miners are to maximize which, being decreasing beyond 1/k, is maximized at x when

When block reward R and network latency l being ratio of connection latency time to block time are considered, the maixmization is about the revenue per unit of time:

It shows that considering latency and R / T being constant for design, the latency ratio shall be as small as ideal which means the block time shall be long rather than short. Further, the optimal x which must be between 0 and 1/k happens when

Two calculation examples assuming zero latency and zero block reward.

• M = 5 mega byte, D = 266 byte, nA = 1000, a miner with h = 10%, then k = 19.71, the optimal x is 0.0486, meaning the tx queue ratio N / nA being 95.79%, the optimal block size being 145.8 mega byte, the loss of production efficiency due to orphan/reorg being 4.17%.
• M = 5 mega byte, D = 266 byte, nA = 100000, a miner with h = 10%, then k = 0.1971, the optimal x is 1.9, meaning the tx queue ratio N / nA being 37.45%, the optimal block size being 5700 mega byte, the loss of production efficiency due to orphan/reorg being 58.97%.

Two calculation examples assuming 0.02 latency and 50 block reward.

• M = 5 mega byte, D = 266 byte, nA = 1000, a miner with h = 10%, then k = 19.71, the optimal x is 0.0164, meaning the tx queue ratio N / nA being 32.32%, the optimal block size being 49.2 mega byte, the loss of production efficiency due to orphan/reorg being 3.16%.
• M = 5 mega byte, D = 266 byte, nA = 100000, a miner with h = 10%, then k = 0.1971, the optimal x is 1.3833E-48, effectively accepts no tx and results in empty blocks and the loss of production efficiency due to orphan/reorg being 1.76% as consequence.

One calculation example of mining monopoly where h is 1.

• The optimal x is 1/k and the miner doesn't care how big/latency a block could be. Even 1/k is greater than 1, the miner simply puts all the transactions during time T into the block and cares nothing for its transmission because the miner is the only mining force, pretty much like a fiat money and the story of some chain.

Note that for generic transaction fee distribution G, the goal is to maximize

and the optimal equation is

and similar stories like the exponential distribution assumption will be told.

Also note that the two maximization using orphan probability vs using efficiency loss agree on the first order by the Taylor series expansion at x = 0 when the miners are small meaning h being almost zero. Again, in a long run the n or A may adapt with the x decided by the miners to have long term kx being 1 and then the expected value becomes . By the point of view of the macro, it is the reduced price of the coin and a regular block fee of qVT. As time goes by, k increases because miners choose higher M for the sake of higher block fee without sacrifice the security as mentioned in AttackCost.

While one may argue that the block size B is not the "transmitted" block size thanks to the fact that miner may see many transactions already, in which only 6 bytes check sum is transmitted rather than the whole D.

It comes to some modeling of probability of knowing at time T of a transaction broadcast at time t during the time interval 0 to T, w(t). Then the average transmitted block size B will be

So the above reasoning remains but for a smaller effective D. For example of a simple modeling, the transaction information before timing t is of the size DnAt and is broadcast to the miner taking time T-t, and all transactions before t are known and all transactions after t are unknown to the miner, therefore

so

And then

And k shall be defined as

Further, the above reasoning assumes that the CPU speed is infinite or the major bottleneck is internet transmission. Otherwise, a CPU speed C for validating the transactions can be introduced as below.

The x in the optimization is the ratio of overall delay time over T beside latency,

where B' be the transmitted block and B be the real block therefore

Therefore

and

In terms of B, the optimal equation is

where

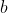The better the infrastructure, the lower b. Beside the theoretical deduction, can be directly observed and and 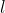can be obtained by regression of block delay time against block size. After that, the optimal block size B, or equivalently the optimal x, is derived accordingly. See OptimalPercentile.

Let r be the block reward of unit time of a design, L be the latency in seconds so that , the above equation does hint about the optimal design about T. At every time interval T, a revenue of

is collected. Knowing that q is also time preference rate, the overall present value of all future revenue is

So the optimal T is about maximization of

whose optimal equation is

When qT is tiny, the left hand side is , this solves to

For example, assume h being zero and x being tiny and L being 10 second and q being 0.005 annually, T is 355168 seconds.