Many forms of money ever found in the history have the rarity characteristic. This is not just coincidence. Suppose the random variable of the amount of the money by one day hard work is X. By rarity, the mean and the deviation of X must be tiny. What is the number of the days that one can collect 1.0 money ?
Denote these identical independent random variables for day i by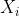 
whose mean and deviation is 
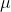and 
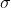. The amount of money one collects in T days is 
. Because collecting more than 1.0 unit in days less or equal than T is equivalent to 
, and the mean is tiny so that the T is supposed to be large, its probability is
%20)
by central limit theorem where N is the standard normal distribution and the T is scattered in a narrow range around 
. To see this, rescale T to another variable R such that 
is mapped to 1.0, therefore the distribution of R is
%20)
Because 
is huge (the definition of 1.0 physical unit allows this number to be arbitrarily large), therefore R who is slightly larger than 1 or smaller than 1 becomes unlikely. Hence the rarity will support a public understanding of the energy amount to get 1.0 unit of that money and establish the proof-of-work property of a sound money.
